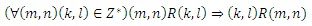2:08:00 PM
|
by Bernad Adjie
Wolfram Mathematica merupakan sebuah aplikasi online yang dapat digunakan untuk menyelesaikan integral tak tentu. Anda dapat menggunakannya di sini.
Aturan dasar dalam penggunaan aplikasi ini antara lain:
Contoh: Ketik sqrt [Sin [x]] untuk akar kuadrat dari sinus dari x.1. Nama fungsi mulai dengan huruf kapital.2. Argumen fungsi ditempatkan di dalam tanda kurung persegi.3. Perkalian ditunjukkan oleh spasi.
Penggunaan operasi dasar adalah sebagai berikut:
+ untuk tambah
- untuk kurang
* atau spasi untuk kali
/ untuk bagi
^ untuk pangkat
sqrt[a] untuk akar
Sedangkan penulisan fungsi trigonometri dan eksponensial yaitu:
Sin[x], Cos[x], Tan[x], Csc[x], Sec[x], Cot[x] untuk fungsi trigonometri (dengan argumen dalam radian)
ArcSin[x], ArcCos[x], ArcTan[x], ArcTan[x,y], ArcCsc[x], ArcSec[x], ArcCot[x] untuk invers dari fungsi trigonometri (dengan hasil dalam radian)
Exp[x] atau E^x untuk fungsi eksponensial
Log[x] untuk logaritma natural
3:19:00 PM
|
by Bernad Adjie
Z* = Z x (Z – {0}) = {(m,n) | m,n Є Z, n ≠ 0}
Didefinisikan relasi R pada Z*
Akan dibuktikan bahwa relasi R merupakan relasi ekuivalensi.
Apakah R reflektif?
Ambil sebarang (m,n) Є Z* maka m.n=m.n (. dalam Z merupakan operasi biner)
Jadi R reflektif.
Apakah R simetris?
Ambil sebarang (m,n),(k,l) Є Z* sedemikian hingga (m,n) R (k,l)
Artinya m.l=n.k
. dalam Z berlaku sifat komutatif sehingga diperoleh
l.m=k.n atau k.n=l.m
Jadi R simetris.
Apakah R transitif?
Ambil sebarang (m,n),(k,l),(x,y) Є Z* dengan (m,n) R (k,l) dan (k,l) R (x,y)
3:39:00 PM
|
by Bernad Adjie
Pengunjung blog tidak hanya berasal dari negara sendiri, melainkan berasal dari berbagai negara di belahan dunia. Lalu pengunjung dari negara mana saja yang pernah mengunjungi blog Anda? Apakah Anda ingin mengetahuinya?
Untuk mengetahuinya, kita dapat menambahkan widget yaitu flag counter. Dengan flag counter kita akan mengetahui jumlah pengunjung suatu blog berikut asal negara yang mengunjungi, seperti yang Anda lihat pada gambar diatas jumlah pengunjung suatu negara ditandai angka dan negara asal pengunjung ditandai dengan gambar bendera sesuai dengan negaranya masing-masing, berikut ini cara memasang widget flag counter pada blog Anda:
1. Klik di sini atau Anda dapat meng-klik widget flag counter pada bagian kanan blog ini.
2. Isi form yang disediakan sesuai keinginan Anda, berapa banyak bendera yang akan ditunjukkan, jumlah kolom termasuk warna background atau tulisan, isi sesuai keinginan Anda, contoh tampilan dapat Anda lihat pada bagian example.
8:41:00 PM
|
by Bernad Adjie
Program segitiga bintang adalah program yang akan menampilkan sebuah segitiga dengan tinggi sesuai keinginan. Segitiga yang dibentuk dapat berupa segitiga siku-siku atau dapat pula segitiga samasisi. Program segitiga bintang ini dapat dibuat dengan beberapa cara, salah satunya dengan struktur perulangan for.
Program segitiga siku-siku
Input:
10
Output:
8:17:00 PM
|
by Bernad Adjie
Pusat massa benda datar dibatasi 0 ≤ r ≤ f(θ), θ Є [α,β]
Perhatikanlah bahwa ∆Ai yang sesuai dengan dA boleh didekati oleh juring dengan radius r* = f(θ*) dan sudut ∆θi atas segitiga samakaki dengan tinggi ri* dan alas ri*∆θi
2:01:00 PM
|
by Bernad Adjie
Sorting adalah proses mengatur sekumpulan objek (contoh : dalam bentuk data) berdasarkan urutan atau susunan tertentu (ascending maupun descending). Jika terdapat N objek yang tersimpan dalam larik L, maka yang disebut urutan ascending adalah jika L[1]≤L[2]≤L[3]≤…≤L[N]. Sedangkan yang disebut sebagai urutan descending adalah apabila L[1]≥L[2]≥L[3]≥…≥L[N].
Dalam program sorting, terdapat beberapa teknik yang bisa digunakan, yaitu maximum sort (selection sort), insertion sort, bubble sort, heap sort, shell sort, quick sort, merge sort, dan radix sort.
Contoh program sorting secara ascending dengan menggunakan teknik bubble dapat didownload
di sini.
Input:
6 (jumlah data atau N)
29 (data ke-1)
27 (data ke-2)
10 (data ke-3)
8 (data ke-4)
76 (data ke-5)
21 (data ke-6)
Output:
8
1:17:00 PM
|
by Bernad Adjie
Teorema Papus Guldin I
Teorema ini memberikan hubungan luas area datar homogen, pusat massa, dan volume benda putaran yang terjadi dengan memutar area tersebut sekeliling sumbu l yang tidak memotong area tersebut.
Teorema:
Volume yang terjadi dari pemutaran area datar homogen sekeliling sumbu l yang tidak memotong area tersebut sebesar hasil kali luas area dan keliling lingkaran dilalui pusat massa area tersebut.
Vl = A . 2 . π . d
d = jarak titik pusat area datar G (x,y) dengan sumbu-l
A = luas area yang diputar
Vl = volume benda putaran sekeliling sumbu-l
Remark:
Jarak titik P (xo,yo) ke garis ax + by + c = 0 sebesar d dengan
Khusus:
11:57:00 AM
|
by Bernad Adjie
Pernahkah Anda berpikir dan bertanya pada diri Anda sendiri “Apa yang membuat orang berterima kasih kepada Anda”? Mengetahui apa yang membuat kita istimewa di hadapan orang lain adalah cara yang hebat untuk meningkatkan rasa kepercayaan diri kita. Jika Anda ingin mengetahui keistimewaan Anda, jawablah pertanyaan-pertanyaan berikut.
1. Tanpa memperhatikan harga mobil, mobil yang paling Anda suka adalah
- Mobil van yang bisa mengangkut banyak orang
- Mobil jeep yang kokoh
- Mobil kecil seperti Mini Cooper atau Beetle
- Mobil ramah lingkungan
- Mobil sport
2.Warna pastel yang Anda suka untuk cat kamar Anda
- Hijau muda
- Putih
- Kuning
- Biru muda
- Peach
3. Anda menggunakan waktu luang/ekstra Anda untuk