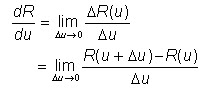|
Turunan biasa dari vektor
Andaikan R(u) suatu vector yang merupakan fungsi dari variable scalar u, maka dirovatif R(u) terhadap u didefinisikan sebagai
R(u) dikatakan terdiferensial terhadap u apabila limit di atas ada.
Mengingat
juga suatu fungsi dari u, maka dapat pula ditentukan derivative order dua atau lebih tinggi,
Kurva-kurva ruang
Apabila R(u) menyatakan vector letak r(u) dengan pangkal vector 0 (titik pangkal sumbu koordinat) dan ujung vector (x,y,z), maka dapat R(u) dapat disajikan sebagai
Dengan demikian derivative r(u) terhadap u dapat disajikan sebagai
Apabila v(t) menyatakan vector kecepatan yang merupakan fungsi dari variable waktu t dan r(t) menyatakan vector letak, maka
menyatakan vector percepatan.
Kontinuitas dan diferensiabilitas
Suatu vector fungsi
dikatakan kontinu di u apabila
atau dengan kata lain
vector fungsi R(u) dikatakan kontinu di u apabila untuk setiap ε > 0 terdapat δ > 0 sedemikian hingga dipenuhi
Vector fungsi
dikatakan terdiferensial terhadap u apabila
atau disajikan sebagai
Rumus diferensiasi
Diberikan vector fungsi
dan fungsi scalar ϕ(u), dipenuhi rumus