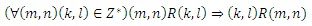|
Z* = Z x (Z – {0}) = {(m,n) | m,n Є Z, n ≠ 0}
Didefinisikan relasi R pada Z*
Akan dibuktikan bahwa relasi R merupakan relasi ekuivalensi.
Apakah R reflektif?
Ambil sebarang (m,n) Є Z* maka m.n=m.n (. dalam Z merupakan operasi biner)
Jadi R reflektif.
Apakah R simetris?
Ambil sebarang (m,n),(k,l) Є Z* sedemikian hingga (m,n) R (k,l)
Artinya m.l=n.k
. dalam Z berlaku sifat komutatif sehingga diperoleh
l.m=k.n atau k.n=l.m
Jadi R simetris.
Apakah R transitif?
Ambil sebarang (m,n),(k,l),(x,y) Є Z* dengan (m,n) R (k,l) dan (k,l) R (x,y)
Artinya m.l=n.k dan k.y=l.xDari m.l=n.k kedua ruas dikalikan dengan y diperoleh
(m.l).y=(n.k).y
Dengan sifat asosiatif dan komutatif pada Z diperoleh
(m.y).l=(n.k).y … (1)
Dari k.y=l.x kedua ruas dikalikan dengan n diperoleh
n.(k.y)=n.(l.x)
Dengan sifat asosiatif dan komutatif pada Z diperoleh
(n.k).y=(n.x).l … (2)
Dari (1) dan (2) diperoleh
(m.y).l=(n.x).l
Dengan sifat kanselatif diperoleh
(m.y)=(n.x)
Jadi R transitif.
Jadi R merupakan relasi ekuivalensi.
Sehingga Z* dapat dipartisi menjadi kelas-kelas yang saling asing.