|
Sistem persamaan linear 3 variabel dalam bentuk standar dapat ditulis Ax+By+Cz=D, dengan x, y, z merupakan variabel dari persamaan tersebut dan A, B, C merupakan koefisien dari variabel yang ada pada persamaan linear tersebut, sedangkan D adalah konstanta. Pada persamaan tersebut A, B, C tidak semuanya nol.
Apabila diberikan 3 persamaan linear dengan 3 variabel, dapat dihitung solusi yang memenuhi persamaan-persamaan tersebut. Banyak cara untuk menyelesaikannya. Bisa menggunakan eliminasi dan substitusi, bisa juga menggunakan operasi baris elementer pada matriks augmented dari persamaan-persamaan tersebut, dan cara yang paling cepat adalah menggunakan aturan Cramer.
Solusi dari 3 persamaan linear dengan 3 variabel belum tentu memiliki solusi tunggal, bahkan ketiga persamaaan tersebut bisa juga tidak memiliki solusi.
Untuk mempermudah dalam mencari solusi dari tiga persamaan dengan 3 variabel dapat dibuat sebuah program dengan bahasa Pascal seperti berikut.
var a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,x,y,z:real;
procedure bacapersamaan;
begin
writeln('persamaan standar Ax+By+Cz=D');
write('masukkan koefisien x dari persamaan pertama :');
readln(a);
write('masukkan koefisien y dari persamaan pertama :');
readln(b);
write('masukkan koefisien z dari persamaan pertama :');
readln(c);
write('masukkan konstanta dari persamaan pertama :');
readln(d);
write('masukkan koefisien x dari persamaan kedua :');
readln(e);
write('masukkan koefisien y dari persamaan kedua :');
readln(f);
write('masukkan koefisien z dari persamaan kedua :');
readln(g);
write('masukkan konstanta dari persamaan kedua :');
readln(h);
write('masukkan koefisien x dari persamaan ketiga :');
readln(i);
write('masukkan koefisien y dari persamaan ketiga :');
readln(j);
write('masukkan koefisien z dari persamaan ketiga :');
readln(k);
write('masukkan konstanta dari persamaan ketiga :');
readln(l);
end;
function determinan(a1,b1,c1,e1,f1,g1,i1,j1,k1:real):real;
begin
determinan:= a1*f1*k1+b1*g1*i1+e1*j1*c1-i1*f1*c1-j1*g1*a1-k1*e1*b1;
end;
function eliminasix(a1,b1,c1,d1:real):real;
begin
eliminasix:=b1*c1-a1*d1;
end;
function eliminasiy(a1,b1,c1,d1,e1,f1:real):real;
begin
eliminasiy:=(c1*d1-a1*f1)/(d1*b1-e1*a1);
end;
function substitusiy(a1,b1,c1,d1:real):real;
begin
substitusiy:=(a1-b1*c1)/d1;
end;
function substitusix(a1,b1,c1,d1,e1,f1:real):real;
begin
substitusix:=(a1-b1*c1-d1*e1)/f1;
end;
begin
bacapersamaan;
if determinan(a,b,c,e,f,g,i,j,k)=0 then
begin
writeln('penyelesaian tidak tunggal atau tidak mempunyai penyelesaian');
end else
begin
m:=eliminasix(a,b,e,f);
n:=eliminasix(a,c,e,g);
o:=eliminasix(a,d,e,h);
p:=eliminasix(a,b,i,j);
q:=eliminasix(a,c,i,k);
r:=eliminasix(a,d,i,l);
z:=eliminasiy(m,n,o,p,q,r);
y:=substitusiy(r,q,z,p);
x:=substitusix(d,b,y,c,z,a);
writeln('nilai x yang memenuhi adalah ',x:0:2);
writeln('nilai y yang memenuhi adalah ',y:0:2);
writeln('nilai z yang memenuhi adalah ',z:0:2);
end;
readln;
end.
Program tersebut menggunakan eliminasi dan substitusi persamaan. Hasil run dari program tersebut dapat dilihat pada gambar di bawah ini.
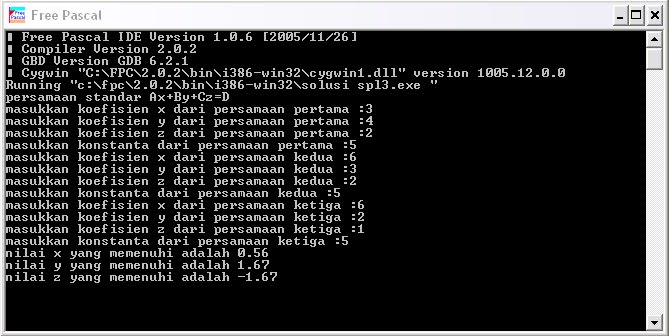
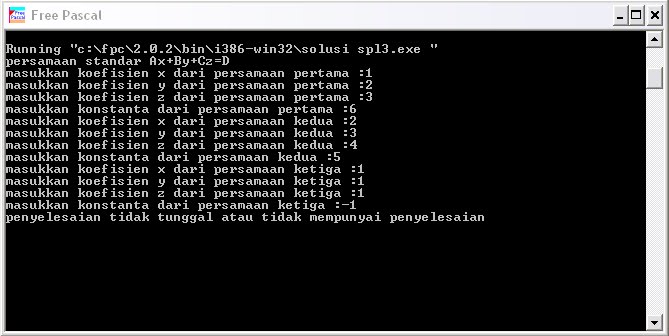
Untuk mendownload program ini dalam format txt, silakan klik di sini.

ini program menggunakan rumus apaan ?
matriks /cramer